厦大数据库实验室博客

总结、分享、收获

实验室主页



Spark 2.1.0 入门：协同过滤算法(Python版)

Ruan Rongcheng (updated: )
大数据学习路线图

【版权声明】博客内容由厦门大学数据库实验室拥有版权，未经允许，请勿转载！

返回Spark教程首页
推荐纸质教材：林子雨、郑海山、赖永炫编著《Spark编程基础（Python版）》

一、方法简介

​ 协同过滤是一种基于一组兴趣相同的用户或项目进行的推荐，它根据邻居用户(与目标用户兴趣相似的用户)的偏好信息产生对目标用户的推荐列表。

关于协同过滤的一个经典的例子就是看电影。如果你不知道哪一部电影是自己喜欢的或者评分比较高的，那么通常的做法就是问问周围的朋友，看看最近有什么好的电影推荐。而在问的时候，肯定都习惯于问跟自己口味差不多的朋友，这就是协同过滤的核心思想。因此，协同过滤是在海量数据中挖掘出小部分与你品味类似的用户，在协同过滤中，这些用户成为邻居，然后根据他们喜欢的东西组织成一个排序的目录推荐给你（如下图所示）。

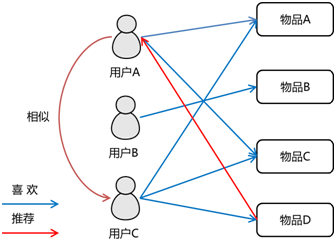
协同过滤算法主要分为基于用户的协同过滤算法和基于项目的协同过滤算法。MLlib当前支持基于模型的协同过滤，其中用户和商品通过一小组隐语义因子进行表达，并且这些因子也用于预测缺失的元素。Spark MLlib实现了 交替最小二乘法 (ALS) 来学习这些隐性语义因子。

二、隐性反馈 vs 显性反馈

显性反馈行为包括用户明确表示对物品喜好的行为，隐性反馈行为指的是那些不能明确反应用户喜好的行为。在许多的现实生活中的很多场景中，我们常常只能接触到隐性的反馈，例如页面游览，点击，购买，喜欢，分享等等。

基于矩阵分解的协同过滤的标准方法，一般将用户商品矩阵中的元素作为用户对商品的显性偏好。在 MLlib 中所用到的处理这种数据的方法来源于文献： Collaborative Filtering for Implicit Feedback Datasets 。 本质上，这个方法将数据作为二元偏好值和偏好强度的一个结合，而不是对评分矩阵直接进行建模。因此，评价就不是与用户对商品的显性评分，而是与所观察到的用户偏好强度关联起来。然后，这个模型将尝试找到隐语义因子来预估一个用户对一个商品的偏好。

示例

下面的例子中，我们将获取MovieLens数据集，其中每行包含一个用户、一个电影、一个该用户对该电影的评分以及时间戳。我们使用默认的ALS.train() 方法，即显性反馈（默认implicitPrefs 为false）来构建推荐模型并根据模型对评分预测的均方根误差来对模型进行评估。

导入需要的包

from pyspark.ml.evaluation import RegressionEvaluator
from pyspark.ml.recommendation import ALS
from pyspark.sql import Row

根据数据结构创建读取规范

创建一个函数，返回即[Int, Int, Float, Long]的对象

def f(x):
    rel = {}
    rel['userId'] = int(x[0])
        rel['movieId'] = int(x[1])
        rel['rating'] = float(x[2])
        rel['timestamp'] = float(x[3])
    return rel

读取数据

ratings = sc.textFile("file:///usr/local/spark/data/mllib/als/sample_movielens_ratings.txt").map(lambda line: line.split('::')).map(lambda p: Row(**f(p))).toDF()

然后把数据打印出来：

ratings.show()


+-------+------+-------------+------+
|movieId|rating|    timestamp|userId|
+-------+------+-------------+------+
|      2|   3.0|1.424380312E9|     0|
|      3|   1.0|1.424380312E9|     0|
|      5|   2.0|1.424380312E9|     0|
|      9|   4.0|1.424380312E9|     0|
|     11|   1.0|1.424380312E9|     0|
|     12|   2.0|1.424380312E9|     0|
|     15|   1.0|1.424380312E9|     0|
|     17|   1.0|1.424380312E9|     0|
|     19|   1.0|1.424380312E9|     0|
|     21|   1.0|1.424380312E9|     0|
|     23|   1.0|1.424380312E9|     0|
|     26|   3.0|1.424380312E9|     0|
|     27|   1.0|1.424380312E9|     0|
|     28|   1.0|1.424380312E9|     0|
|     29|   1.0|1.424380312E9|     0|
|     30|   1.0|1.424380312E9|     0|
|     31|   1.0|1.424380312E9|     0|
|     34|   1.0|1.424380312E9|     0|
|     37|   1.0|1.424380312E9|     0|
|     41|   2.0|1.424380312E9|     0|
+-------+------+-------------+------+
only showing top 20 rows

构建模型

把MovieLens数据集划分训练集和测试集

training, test = ratings.randomSplit([0.8,0.2])

使用ALS来建立推荐模型，这里我们构建了两个模型，一个是显性反馈，一个是隐性反馈

alsExplicit  = ALS(maxIter=5, regParam=0.01, userCol="userId", itemCol="movieId", ratingCol="rating")
alsImplicit = ALS(maxIter=5, regParam=0.01, implicitPrefs=True,userCol="userId", itemCol="movieId", ratingCol="rating")

在 ML 中的实现有如下的参数:

numBlocks 是用于并行化计算的用户和商品的分块个数 (默认为10)。
rank 是模型中隐语义因子的个数（默认为10）。
maxIter 是迭代的次数（默认为10）。
regParam 是ALS的正则化参数（默认为1.0）。
implicitPrefs 决定了是用显性反馈ALS的版本还是用适用隐性反馈数据集的版本（默认是false，即用显性反馈）。
alpha 是一个针对于隐性反馈 ALS 版本的参数，这个参数决定了偏好行为强度的基准（默认为1.0）。
nonnegative 决定是否对最小二乘法使用非负的限制（默认为false）。
​ 可以调整这些参数，不断优化结果，使均方差变小。比如：imaxIter越大，regParam越 小，均方差会越小，推荐结果较优。

接下来，把推荐模型放在训练数据上训练：

modelExplicit = alsExplicit.fit(training)
modelImplicit = alsImplicit.fit(training)

模型预测

使用训练好的推荐模型对测试集中的用户商品进行预测评分，得到预测评分的数据集

predictionsExplicit = modelExplicit.transform(test)
predictionsImplicit = modelImplicit.transform(test)

我们把结果输出，对比一下真实结果与预测结果：

predictionsExplicit.show()

+-------+------+-------------+------+-----------+                               
|movieId|rating|    timestamp|userId| prediction|
+-------+------+-------------+------+-----------+
|     31|   4.0|1.424380312E9|    12|  1.6642745|
|     31|   1.0|1.424380312E9|    13|  2.4953516|
|     31|   1.0|1.424380312E9|    24|   1.065728|
|     31|   1.0|1.424380312E9|     0| 0.27203378|
|     85|   1.0|1.424380312E9|    28| -4.3580985|
|     85|   1.0|1.424380312E9|    12| 0.40682888|
|     85|   1.0|1.424380312E9|    13|   3.660988|
|     85|   2.0|1.424380312E9|    20|  2.8040016|
|     85|   1.0|1.424380312E9|     5|  1.5130293|
|     85|   5.0|1.424380312E9|     8|  4.2697716|
|     85|   1.0|1.424380312E9|    29|-0.08079797|
|     65|   5.0|1.424380312E9|    23|   2.085921|
|     65|   1.0|1.424380312E9|    24| 0.24009112|
|     53|   1.0|1.424380312E9|    23| -1.0775211|
|     53|   1.0|1.424380312E9|    25|  0.9550235|
|     78|   1.0|1.424380312E9|    28|-0.26401743|
|     78|   1.0|1.424380312E9|    22| 0.60926896|
|     78|   1.0|1.424380312E9|    20| 0.12379208|
|     34|   1.0|1.424380312E9|    14| -0.2330051|
|     81|   3.0|1.424380312E9|    26|   5.684144|
+-------+------+-------------+------+-----------+
only showing top 20 rows



predictionsImplicit.show()

+-------+------+-------------+------+-----------+                               
|movieId|rating|    timestamp|userId| prediction|
+-------+------+-------------+------+-----------+
|     31|   4.0|1.424380312E9|    12|0.012495369|
|     31|   1.0|1.424380312E9|    13| 0.29184195|
|     31|   1.0|1.424380312E9|    24|0.030779492|
|     31|   1.0|1.424380312E9|     0|-0.11765161|
|     85|   1.0|1.424380312E9|    28|  0.7986825|
|     85|   1.0|1.424380312E9|    12| 0.43071586|
|     85|   1.0|1.424380312E9|    13|-0.43334037|
|     85|   2.0|1.424380312E9|    20| 0.41960382|
|     85|   1.0|1.424380312E9|     5|-0.18235317|
|     85|   5.0|1.424380312E9|     8| 0.15960173|
|     85|   1.0|1.424380312E9|    29|0.087186486|
|     65|   5.0|1.424380312E9|    23| 0.93609256|
|     65|   1.0|1.424380312E9|    24| 0.21193008|
|     53|   1.0|1.424380312E9|    23| 0.30090192|
|     53|   1.0|1.424380312E9|    25| 0.07434524|
|     78|   1.0|1.424380312E9|    28| -0.3169421|
|     78|   1.0|1.424380312E9|    22|  0.4639935|
|     78|   1.0|1.424380312E9|    20|  0.5240105|
|     34|   1.0|1.424380312E9|    14|0.116244696|
|     81|   3.0|1.424380312E9|    26|  0.3299607|
+-------+------+-------------+------+-----------+
only showing top 20 rows

模型评估

通过计算模型的均方根误差来对模型进行评估，均方根误差越小，模型越准确：

evaluator = RegressionEvaluator().setMetricName("rmse").setLabelCol("rating").setPredictionCol("prediction")

打印出两个模型的均方根误差 ：

print("Explicit:Root-mean-square error = "+str(rmseExplicit))
Explicit:Root-mean-square error = 1.9093067340213505
print("Explicit:Root-mean-square error = "+str(rmseImplicit))
Implicit:Root-mean-square error = 1.9965886603519194
© 2014 厦大数据库实验室