厦大数据库实验室博客

总结、分享、收获

实验室主页



Spark2.1.0入门：逻辑斯蒂回归分类器(Python版)

Ruan Rongcheng (updated: )
大数据学习路线图

【版权声明】博客内容由厦门大学数据库实验室拥有版权，未经允许，请勿转载！

[返回Spark教程首页]
推荐纸质教材：林子雨、郑海山、赖永炫编著《Spark编程基础（Python版）》

逻辑斯蒂回归

方法简介

​ 逻辑斯蒂回归（logistic regression）是统计学习中的经典分类方法，属于对数线性模型。logistic回归的因变量可以是二分类的，也可以是多分类的。

基本原理

logistic分布

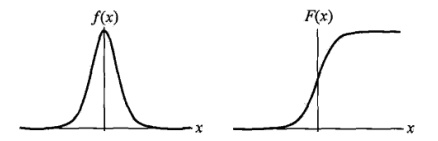
​ 设X是连续随机变量，X服从logistic分布是指X具有下列分布函数和密度函数：

​

    \[F(x)=P(x \le x)=\frac 1 {1+e^{-(x-\mu)/\gamma}}\]

​

    \[f(x)=F^{'}(x)=\frac {e^{-(x-\mu)/\gamma}} {\gamma(1+e^{-(x-\mu)/\gamma})^2}\]

​ 其中，\mu为位置参数，\gamma为形状参数。

​ f(x)与

    \[F(x)\]

图像如下，其中分布函数是以

    \[(\mu, \frac 1 2)\]

为中心对阵，

    \[\gamma\]

$越小曲线变化越快。

二项logistic回归模型：

​ 二项logistic回归模型如下：

​

    \[P(Y=1|x)=\frac {exp(w \cdot x + b)} {1 + exp(w \cdot x + b)}\]

​

    \[P(Y=0|x)=\frac {1} {1 + exp(w \cdot x + b)}\]

​ 其中，

    \[x \in R^n\]

是输入，

    \[Y \in {0,1}\]

是输出，w称为权值向量，b称为偏置，

    \[w \cdot x\]

为w和x的内积。

参数估计

​ 假设：

​

    \[P(Y=1|x)=\pi (x), \quad P(Y=0|x)=1-\pi (x)\]

​ 则似然函数为:

​

    \[\prod_{i=1}^N [\pi (x_i)]^{y_i} [1 - \pi(x_i)]^{1-y_i}\]

​ 求对数似然函数：

​

    \[L(w) = \sum_{i=1}^N [y_i \log{\pi(x_i)} + (1-y_i) \log{(1 - \pi(x_i)})]\]

​

    \[\sum_{i=1}^N [y_i \log{\frac {\pi (x_i)} {1 - \pi(x_i)}} + \log{(1 - \pi(x_i)})]=\sum_{i=1}^N [y_i \log{\frac {\pi (x_i)} {1 - \pi(x_i)}} + \log{(1 - \pi(x_i)})]\]

​ 从而对

    \[L(w)\]

求极大值，得到w的估计值。求极值的方法可以是梯度下降法，梯度上升法等。

示例代码

​ 我们以iris数据集（iris）为例进行分析。iris以鸢尾花的特征作为数据来源，数据集包含150个数据集，分为3类，每类50个数据，每个数据包含4个属性，是在数据挖掘、数据分类中非常常用的测试集、训练集。为了便于理解，我们这里主要用后两个属性（花瓣的长度和宽度）来进行分类。目前 spark.ml 中支持二分类和多分类，我们将分别从“用二项逻辑斯蒂回归来解决二分类问题”、“用多项逻辑斯蒂回归来解决二分类问题”、“用多项逻辑斯蒂回归来解决多分类问题”三个方面进行分析。

用二项逻辑斯蒂回归解决 二分类 问题

首先我们先取其中的后两类数据，用二项逻辑斯蒂回归进行二分类分析。

1. 导入需要的包：
from pyspark.sql import Row,functions
from pyspark.ml.linalg import Vector,Vectors
from pyspark.ml.evaluation import MulticlassClassificationEvaluator
from pyspark.ml import Pipeline
from pyspark.ml.feature import IndexToString, StringIndexer, VectorIndexer,HashingTF, Tokenizer
from pyspark.ml.classification import LogisticRegression,LogisticRegressionModel,BinaryLogisticRegressionSummary, LogisticRegression
2. 读取数据，简要分析：

​ 我们定制一个函数，来返回一个指定的数据，然后读取文本文件，第一个map把每行的数据用“,”隔开，比如在我们的数据集中，每行被分成了5部分，前4部分是鸢尾花的4个特征，最后一部分是鸢尾花的分类；我们这里把特征存储在Vector中，创建一个Iris模式的RDD，然后转化成dataframe；最后调用show()方法来查看一下部分数据。

def f(x):
    rel = {}
    rel['features'] = Vectors.dense(float(x[0]),float(x[1]),float(x[2]),float(x[3]))
    rel['label'] = str(x[4])
    return rel

data = spark.sparkContext.textFile("file:///usr/local/spark/iris.txt").map(lambda line: line.split(',')).map(lambda p: Row(**f(p))).toDF()

+-----------------+-----------+
|         features|      label|
+-----------------+-----------+
|[5.1,3.5,1.4,0.2]|Iris-setosa|
|[4.9,3.0,1.4,0.2]|Iris-setosa|
|[4.7,3.2,1.3,0.2]|Iris-setosa|
|[4.6,3.1,1.5,0.2]|Iris-setosa|
|[5.0,3.6,1.4,0.2]|Iris-setosa|
|[5.4,3.9,1.7,0.4]|Iris-setosa|
|[4.6,3.4,1.4,0.3]|Iris-setosa|
|[5.0,3.4,1.5,0.2]|Iris-setosa|
|[4.4,2.9,1.4,0.2]|Iris-setosa|
|[4.9,3.1,1.5,0.1]|Iris-setosa|
|[5.4,3.7,1.5,0.2]|Iris-setosa|
|[4.8,3.4,1.6,0.2]|Iris-setosa|
|[4.8,3.0,1.4,0.1]|Iris-setosa|
|[4.3,3.0,1.1,0.1]|Iris-setosa|
|[5.8,4.0,1.2,0.2]|Iris-setosa|
|[5.7,4.4,1.5,0.4]|Iris-setosa|
|[5.4,3.9,1.3,0.4]|Iris-setosa|
|[5.1,3.5,1.4,0.3]|Iris-setosa|
|[5.7,3.8,1.7,0.3]|Iris-setosa|
|[5.1,3.8,1.5,0.3]|Iris-setosa|
+-----------------+-----------+
only showing top 20 rows

​ 因为我们现在处理的是2分类问题，所以我们不需要全部的3类数据，我们要从中选出两类的数据。这里首先把刚刚得到的数据注册成一个表iris，注册成这个表之后，我们就可以通过sql语句进行数据查询，比如我们这里选出了所有不属于“Iris-setosa”类别的数据；选出我们需要的数据后，我们可以把结果打印出来看一下，这时就已经没有“Iris-setosa”类别的数据。

data.createOrReplaceTempView("iris")
df = spark.sql("select * from iris where label != 'Iris-setosa'")
rel = df.rdd.map(lambda t : str(t[1])+":"+str(t[0])).collect()
for item in rel:
            print(item)

Iris-versicolor:[7.0,3.2,4.7,1.4]
Iris-versicolor:[6.4,3.2,4.5,1.5]
Iris-versicolor:[6.9,3.1,4.9,1.5]
Iris-versicolor:[5.5,2.3,4.0,1.3]
Iris-versicolor:[6.5,2.8,4.6,1.5]
Iris-versicolor:[5.7,2.8,4.5,1.3]
Iris-versicolor:[6.3,3.3,4.7,1.6]
Iris-versicolor:[4.9,2.4,3.3,1.0]
Iris-versicolor:[6.6,2.9,4.6,1.3]
Iris-versicolor:[5.2,2.7,3.9,1.4]
Iris-versicolor:[5.0,2.0,3.5,1.0]
Iris-versicolor:[5.9,3.0,4.2,1.5]
Iris-versicolor:[6.0,2.2,4.0,1.0]
Iris-versicolor:[6.1,2.9,4.7,1.4]
Iris-versicolor:[5.6,2.9,3.6,1.3]
Iris-versicolor:[6.7,3.1,4.4,1.4]
Iris-versicolor:[5.6,3.0,4.5,1.5]
Iris-versicolor:[5.8,2.7,4.1,1.0]
Iris-versicolor:[6.2,2.2,4.5,1.5]
Iris-versicolor:[5.6,2.5,3.9,1.1]
Iris-versicolor:[5.9,3.2,4.8,1.8]
Iris-versicolor:[6.1,2.8,4.0,1.3]
Iris-versicolor:[6.3,2.5,4.9,1.5]
Iris-versicolor:[6.1,2.8,4.7,1.2]
Iris-versicolor:[6.4,2.9,4.3,1.3]
Iris-versicolor:[6.6,3.0,4.4,1.4]
Iris-versicolor:[6.8,2.8,4.8,1.4]
Iris-versicolor:[6.7,3.0,5.0,1.7]
Iris-versicolor:[6.0,2.9,4.5,1.5]
Iris-versicolor:[5.7,2.6,3.5,1.0]
Iris-versicolor:[5.5,2.4,3.8,1.1]
Iris-versicolor:[5.5,2.4,3.7,1.0]
Iris-versicolor:[5.8,2.7,3.9,1.2]
Iris-versicolor:[6.0,2.7,5.1,1.6]
Iris-versicolor:[5.4,3.0,4.5,1.5]
Iris-versicolor:[6.0,3.4,4.5,1.6]
Iris-versicolor:[6.7,3.1,4.7,1.5]
Iris-versicolor:[6.3,2.3,4.4,1.3]
Iris-versicolor:[5.6,3.0,4.1,1.3]
Iris-versicolor:[5.5,2.5,4.0,1.3]
Iris-versicolor:[5.5,2.6,4.4,1.2]
Iris-versicolor:[6.1,3.0,4.6,1.4]
Iris-versicolor:[5.8,2.6,4.0,1.2]
Iris-versicolor:[5.0,2.3,3.3,1.0]
Iris-versicolor:[5.6,2.7,4.2,1.3]
Iris-versicolor:[5.7,3.0,4.2,1.2]
Iris-versicolor:[5.7,2.9,4.2,1.3]
Iris-versicolor:[6.2,2.9,4.3,1.3]
Iris-versicolor:[5.1,2.5,3.0,1.1]
Iris-versicolor:[5.7,2.8,4.1,1.3]
Iris-virginica:[6.3,3.3,6.0,2.5]
Iris-virginica:[5.8,2.7,5.1,1.9]
Iris-virginica:[7.1,3.0,5.9,2.1]
Iris-virginica:[6.3,2.9,5.6,1.8]
Iris-virginica:[6.5,3.0,5.8,2.2]
Iris-virginica:[7.6,3.0,6.6,2.1]
Iris-virginica:[4.9,2.5,4.5,1.7]
Iris-virginica:[7.3,2.9,6.3,1.8]
Iris-virginica:[6.7,2.5,5.8,1.8]
Iris-virginica:[7.2,3.6,6.1,2.5]
Iris-virginica:[6.5,3.2,5.1,2.0]
Iris-virginica:[6.4,2.7,5.3,1.9]
Iris-virginica:[6.8,3.0,5.5,2.1]
Iris-virginica:[5.7,2.5,5.0,2.0]
Iris-virginica:[5.8,2.8,5.1,2.4]
Iris-virginica:[6.4,3.2,5.3,2.3]
Iris-virginica:[6.5,3.0,5.5,1.8]
Iris-virginica:[7.7,3.8,6.7,2.2]
Iris-virginica:[7.7,2.6,6.9,2.3]
Iris-virginica:[6.0,2.2,5.0,1.5]
Iris-virginica:[6.9,3.2,5.7,2.3]
Iris-virginica:[5.6,2.8,4.9,2.0]
Iris-virginica:[7.7,2.8,6.7,2.0]
Iris-virginica:[6.3,2.7,4.9,1.8]
Iris-virginica:[6.7,3.3,5.7,2.1]
Iris-virginica:[7.2,3.2,6.0,1.8]
Iris-virginica:[6.2,2.8,4.8,1.8]
Iris-virginica:[6.1,3.0,4.9,1.8]
Iris-virginica:[6.4,2.8,5.6,2.1]
Iris-virginica:[7.2,3.0,5.8,1.6]
Iris-virginica:[7.4,2.8,6.1,1.9]
Iris-virginica:[7.9,3.8,6.4,2.0]
Iris-virginica:[6.4,2.8,5.6,2.2]
Iris-virginica:[6.3,2.8,5.1,1.5]
Iris-virginica:[6.1,2.6,5.6,1.4]
Iris-virginica:[7.7,3.0,6.1,2.3]
Iris-virginica:[6.3,3.4,5.6,2.4]
Iris-virginica:[6.4,3.1,5.5,1.8]
Iris-virginica:[6.0,3.0,4.8,1.8]
Iris-virginica:[6.9,3.1,5.4,2.1]
Iris-virginica:[6.7,3.1,5.6,2.4]
Iris-virginica:[6.9,3.1,5.1,2.3]
Iris-virginica:[5.8,2.7,5.1,1.9]
Iris-virginica:[6.8,3.2,5.9,2.3]
Iris-virginica:[6.7,3.3,5.7,2.5]
Iris-virginica:[6.7,3.0,5.2,2.3]
Iris-virginica:[6.3,2.5,5.0,1.9]
Iris-virginica:[6.5,3.0,5.2,2.0]
Iris-virginica:[6.2,3.4,5.4,2.3]
Iris-virginica:[5.9,3.0,5.1,1.8]
3. 构建ML的pipeline

​ 分别获取标签列和特征列，进行索引，并进行了重命名。

labelIndexer = StringIndexer().setInputCol("label").setOutputCol("indexedLabel").fit(df)
featureIndexer = VectorIndexer().setInputCol("features").setOutputCol("indexedFeatures").fit(df)
featureIndexer: org.apache.spark.ml.feature.VectorIndexerModel = vecIdx_53b988077b38

​ 接下来，我们把数据集随机分成训练集和测试集，其中训练集占70%。

trainingData, testData = df.randomSplit([0.7,0.3])

​ 然后，我们设置logistic的参数，这里我们统一用setter的方法来设置，也可以用ParamMap来设置（具体的可以查看spark mllib的官网）。这里我们设置了循环次数为10次，正则化项为0.3等，具体的可以设置的参数可以通过explainParams()来获取，还能看到我们已经设置的参数的结果。

lr = LogisticRegression().setLabelCol("indexedLabel").setFeaturesCol("indexedFeatures").setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8)
print("LogisticRegression parameters:\n" + lr.explainParams())

LogisticRegression parameters:
aggregationDepth: suggested depth for treeAggregate (>= 2). (default: 2)
elasticNetParam: the ElasticNet mixing parameter, in range [0, 1]. For alpha = 0, the penalty is an L2 penalty. For alpha = 1, it is an L1 penalty. (default: 0.0, current: 0.8)
family: The name of family which is a description of the label distribution to be used in the model. Supported options: auto, binomial, multinomial (default: auto)
featuresCol: features column name. (default: features, current: indexedFeatures)
fitIntercept: whether to fit an intercept term. (default: True)
labelCol: label column name. (default: label, current: indexedLabel)
maxIter: max number of iterations (>= 0). (default: 100, current: 10)
predictionCol: prediction column name. (default: prediction)
probabilityCol: Column name for predicted class conditional probabilities. Note: Not all models output well-calibrated probability estimates! These probabilities should be treated as confidences, not precise probabilities. (default: probability)
rawPredictionCol: raw prediction (a.k.a. confidence) column name. (default: rawPrediction)
regParam: regularization parameter (>= 0). (default: 0.0, current: 0.3)
standardization: whether to standardize the training features before fitting the model. (default: True)
threshold: Threshold in binary classification prediction, in range [0, 1]. If threshold and thresholds are both set, they must match.e.g. if threshold is p, then thresholds must be equal to [1-p, p]. (default: 0.5)
thresholds: Thresholds in multi-class classification to adjust the probability of predicting each class. Array must have length equal to the number of classes, with values > 0, excepting that at most one value may be 0. The class with largest value p/t is predicted, where p is the original probability of that class and t is the class's threshold. (undefined)
tol: the convergence tolerance for iterative algorithms (>= 0). (default: 1e-06)
weightCol: weight column name. If this is not set or empty, we treat all instance weights as 1.0. (undefined)

​ 这里我们设置一个labelConverter，目的是把预测的类别重新转化成字符型的。

labelConverter = IndexToString().setInputCol("prediction").setOutputCol("predictedLabel").setLabels(labelIndexer.labels)

​ 构建pipeline，设置stage，然后调用fit()来训练模型。

lrPipeline =  Pipeline().setStages([labelIndexer, featureIndexer, lr, labelConverter])
lrPipelineModel = lrPipeline.fit(trainingData)

​ pipeline本质上是一个Estimator，当pipeline调用fit()的时候就产生了一个PipelineModel，本质上是一个Transformer。然后这个PipelineModel就可以调用transform()来进行预测，生成一个新的DataFrame，即利用训练得到的模型对测试集进行验证。

lrPredictions = lrPipelineModel.transform(testData)

​ 最后我们可以输出预测的结果，其中select选择要输出的列，collect获取所有行的数据，用foreach把每行打印出来。其中打印出来的值依次分别代表该行数据的真实分类和特征值、预测属于不同分类的概率、预测的分类。

preRel = lrPredictions.select("predictedLabel", "label", "features", "probability").collect()
for item in preRel:
    print(str(item['label'])+','+str(item['features'])+'-->prob='+str(item['probability'])+',predictedLabel'+str(item['predictedLabel']))

Iris-versicolor,[5.2,2.7,3.9,1.4]-->prob=[0.474125433289,0.525874566711],predictedLabelIris-virginica
Iris-versicolor,[5.5,2.3,4.0,1.3]-->prob=[0.498724224708,0.501275775292],predictedLabelIris-virginica
Iris-versicolor,[5.6,3.0,4.5,1.5]-->prob=[0.456659495584,0.543340504416],predictedLabelIris-virginica
Iris-versicolor,[5.9,3.2,4.8,1.8]-->prob=[0.396329949568,0.603670050432],predictedLabelIris-virginica
Iris-versicolor,[6.3,3.3,4.7,1.6]-->prob=[0.442287021876,0.557712978124],predictedLabelIris-virginica
Iris-versicolor,[6.4,2.9,4.3,1.3]-->prob=[0.507813688472,0.492186311528],predictedLabelIris-versicolor
Iris-versicolor,[6.7,3.0,5.0,1.7]-->prob=[0.42504596458,0.57495403542],predictedLabelIris-virginica
Iris-virginica,[4.9,2.5,4.5,1.7]-->prob=[0.407378398796,0.592621601204],predictedLabelIris-virginica
Iris-versicolor,[5.5,2.4,3.8,1.1]-->prob=[0.541810138118,0.458189861882],predictedLabelIris-versicolor
Iris-versicolor,[5.5,2.5,4.0,1.3]-->prob=[0.498724224708,0.501275775292],predictedLabelIris-virginica
Iris-versicolor,[5.5,2.6,4.4,1.2]-->prob=[0.520304937567,0.479695062433],predictedLabelIris-versicolor
Iris-versicolor,[5.7,2.6,3.5,1.0]-->prob=[0.565147445416,0.434852554584],predictedLabelIris-versicolor
Iris-versicolor,[5.8,2.7,3.9,1.2]-->prob=[0.523329193496,0.476670806504],predictedLabelIris-versicolor
Iris-virginica,[5.8,2.7,5.1,1.9]-->prob=[0.374915000487,0.625084999513],predictedLabelIris-virginica
Iris-virginica,[5.8,2.8,5.1,2.4]-->prob=[0.280289494118,0.719710505882],predictedLabelIris-virginica
Iris-versicolor,[6.0,2.7,5.1,1.6]-->prob=[0.43929948357,0.56070051643],predictedLabelIris-virginica
Iris-virginica,[6.1,3.0,4.9,1.8]-->prob=[0.398264741954,0.601735258046],predictedLabelIris-virginica
Iris-virginica,[6.3,2.8,5.1,1.5]-->prob=[0.463684596073,0.536315403927],predictedLabelIris-virginica
Iris-virginica,[6.3,3.3,6.0,2.5]-->prob=[0.267137732158,0.732862267842],predictedLabelIris-virginica
Iris-virginica,[6.5,3.0,5.2,2.0]-->prob=[0.361404006967,0.638595993033],predictedLabelIris-virginica
Iris-virginica,[6.5,3.0,5.5,1.8]-->prob=[0.402143821718,0.597856178282],predictedLabelIris-virginica
Iris-virginica,[6.7,2.5,5.8,1.8]-->prob=[0.404087997603,0.595912002397],predictedLabelIris-virginica
Iris-virginica,[6.9,3.1,5.4,2.1]-->prob=[0.345363437071,0.654636562929],predictedLabelIris-virginica
Iris-virginica,[7.3,2.9,6.3,1.8]-->prob=[0.409938392379,0.590061607621],predictedLabelIris-virginica
Iris-virginica,[7.4,2.8,6.1,1.9]-->prob=[0.390181923993,0.609818076007],predictedLabelIris-virginica
4. 模型评估

​ 创建一个MulticlassClassificationEvaluator实例，用setter方法把预测分类的列名和真实分类的列名进行设置；然后计算预测准确率和错误率。

evaluator = MulticlassClassificationEvaluator().setLabelCol("indexedLabel").setPredictionCol("prediction")
lrAccuracy = evaluator.evaluate(lrPredictions)
print("Test Error = " + str(1.0 - lrAccuracy))
Test Error = 0.35111111111111115

​ 从上面可以看到预测的准确性达到65%，接下来我们可以通过model来获取我们训练得到的逻辑斯蒂模型。前面已经说过model是一个PipelineModel，因此我们可以通过调用它的stages来获取模型，具体如下：

lrModel = lrPipelineModel.stages[2]
print("Coefficients: " + str(lrModel.coefficients)+"Intercept: "+str(lrModel.intercept)+"numClasses: "+str(lrModel.numClasses)+"numFeatures: "+str(lrModel.numFeatures))
Coefficients: [-0.0396171957643483,0.0,0.0,0.07240315639651046]Intercept: -0.23127346342015379numClasses: 2numFeatures: 4
5. 模型评估

​ spark的ml库还提供了一个对模型的摘要总结（summary），不过目前只支持二项逻辑斯蒂回归，而且要显示转化成BinaryLogisticRegressionSummary 。在下面的代码中，首先获得二项逻辑斯模型的摘要；然后获得10次循环中损失函数的变化，并将结果打印出来，可以看到损失函数随着循环是逐渐变小的，损失函数越小，模型就越好；接下来，我们把摘要强制转化为BinaryLogisticRegressionSummary ，来获取用来评估模型性能的矩阵；通过获取ROC，我们可以判断模型的好坏，areaUnderROC达到了 0.969551282051282，说明我们的分类器还是不错的；最后，我们通过最大化fMeasure来选取最合适的阈值，其中fMeasure是一个综合了召回率和准确率的指标，通过最大化fMeasure，我们可以选取到用来分类的最合适的阈值。

trainingSummary = lrModel.summary
objectiveHistory = trainingSummary.objectiveHistory
for item in objectiveHistory:
...     print(item)
... 
0.6930582890371242
0.6899151958544979
0.6884360489604017
0.6866214680339037
0.6824264404293411
0.6734525297891238
0.6718869589782477
0.6700321119842002
0.6681741952485035
0.6668744860924799
0.6656055740433819


print(trainingSummary.areaUnderROC)
0.9889758179231863

fMeasure = trainingSummary.fMeasureByThreshold

maxFMeasure = fMeasure.select(functions.max("F-Measure")).head()[0]
0.9599999999999999

bestThreshold = fMeasure.where(fMeasure["F-Measure"]== maxFMeasure).select("threshold").head()[0]
0.5487261156903904

lr.setThreshold(bestThreshold)

用多项逻辑斯蒂回归解决 二分类 问题

​ 对于二分类问题，我们还可以用多项逻辑斯蒂回归进行多分类分析。多项逻辑斯蒂回归与二项逻辑斯蒂回归类似，只是在模型设置上把family参数设置成multinomial，这里我们仅列出结果：

mlr =  LogisticRegression().setLabelCol("indexedLabel").setFeaturesCol("indexedFeatures").setMaxIter(10).setRegParam(0.3).setElasticNetParam(0.8).setFamily("multinomial")

mlrPipeline = Pipeline().setStages([labelIndexer, featureIndexer, mlr, labelConverter])

mlrPipelineModel = mlrPipeline.fit(trainingData)

mlrPreRel = mlrPredictions.select("predictedLabel", "label", "features", "probability").collect()
for item in mlrPreRel:
    print('('+str(item['label'])+','+str(item['features'])+')-->prob='+str(item['probability'])+',predictLabel='+str(item['predictedLabel']))

(Iris-versicolor,[5.2,2.7,3.9,1.4])-->prob=[0.769490937876,0.230509062124],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.3,4.0,1.3])-->prob=[0.795868931454,0.204131068546],predictLabel=Iris-versicolor
(Iris-versicolor,[5.6,3.0,4.5,1.5])-->prob=[0.740814410092,0.259185589908],predictLabel=Iris-versicolor
(Iris-versicolor,[5.9,3.2,4.8,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-versicolor,[6.3,3.3,4.7,1.6])-->prob=[0.709915262079,0.290084737921],predictLabel=Iris-versicolor
(Iris-versicolor,[6.4,2.9,4.3,1.3])-->prob=[0.795868931454,0.204131068546],predictLabel=Iris-versicolor
(Iris-versicolor,[6.7,3.0,5.0,1.7])-->prob=[0.676938845836,0.323061154164],predictLabel=Iris-versicolor
(Iris-virginica,[4.9,2.5,4.5,1.7])-->prob=[0.676938845836,0.323061154164],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.4,3.8,1.1])-->prob=[0.841727580252,0.158272419748],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.5,4.0,1.3])-->prob=[0.795868931454,0.204131068546],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.6,4.4,1.2])-->prob=[0.819934748118,0.180065251882],predictLabel=Iris-versicolor
(Iris-versicolor,[5.7,2.6,3.5,1.0])-->prob=[0.861328953172,0.138671046828],predictLabel=Iris-versicolor
(Iris-versicolor,[5.8,2.7,3.9,1.2])-->prob=[0.819934748118,0.180065251882],predictLabel=Iris-versicolor
(Iris-virginica,[5.8,2.7,5.1,1.9])-->prob=[0.605700014665,0.394299985335],predictLabel=Iris-versicolor
(Iris-virginica,[5.8,2.8,5.1,2.4])-->prob=[0.414135982436,0.585864017564],predictLabel=Iris-virginica
(Iris-versicolor,[6.0,2.7,5.1,1.6])-->prob=[0.709915262079,0.290084737921],predictLabel=Iris-versicolor
(Iris-virginica,[6.1,3.0,4.9,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[6.3,2.8,5.1,1.5])-->prob=[0.740814410092,0.259185589908],predictLabel=Iris-versicolor
(Iris-virginica,[6.3,3.3,6.0,2.5])-->prob=[0.377041048688,0.622958951312],predictLabel=Iris-virginica
(Iris-virginica,[6.5,3.0,5.2,2.0])-->prob=[0.568084351171,0.431915648829],predictLabel=Iris-versicolor
(Iris-virginica,[6.5,3.0,5.5,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[6.7,2.5,5.8,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[6.9,3.1,5.4,2.1])-->prob=[0.529666704954,0.470333295046],predictLabel=Iris-versicolor
(Iris-virginica,[7.3,2.9,6.3,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[7.4,2.8,6.1,1.9])-->prob=[0.605700014665,0.394299985335],predictLabel=Iris-versicolor

mlrAccuracy = evaluator.evaluate(mlrPredictions)

print("Test Error = " + str(1.0 - mlrAccuracy))

Test Error = 0.48730158730158735


mlrModel = mlrPipelineModel.stages[2]

print("Multinomial coefficients: " +str(mlrModel.coefficientMatrix)+"Multin
omial intercepts: "+str(mlrModel.interceptVector)+"numClasses: "+str(mlrModel.numClasses)+
"numFeatures: "+str(mlrModel.numFeatures))

Multinomial coefficients: 2 X 4 CSRMatrix
(0,3) -0.0776
(1,3) 0.0776Multinomial intercepts: [0.913185966051,-0.913185966051]numClasses: 2numFeatures: 4

用多项逻辑斯蒂回归解决 多分类 问题

​ 对于多分类问题，我们需要用多项逻辑斯蒂回归进行多分类分析。这里我们用全部的iris数据集，即有三个类别，过程与上述基本一致，这里我们同样仅列出结果：

mlrPreRel = mlrPredictions.select("predictedLabel", "label", "features", "probability").collect()
for item in mlrPreRel:
    print('('+str(item['label'])+','+str(item['features'])+')-->prob='+str(item['probability'])+',predictLabel='+str(item['predictedLabel']))

(Iris-versicolor,[5.2,2.7,3.9,1.4])-->prob=[0.769490937876,0.230509062124],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.3,4.0,1.3])-->prob=[0.795868931454,0.204131068546],predictLabel=Iris-versicolor
(Iris-versicolor,[5.6,3.0,4.5,1.5])-->prob=[0.740814410092,0.259185589908],predictLabel=Iris-versicolor
(Iris-versicolor,[5.9,3.2,4.8,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-versicolor,[6.3,3.3,4.7,1.6])-->prob=[0.709915262079,0.290084737921],predictLabel=Iris-versicolor
(Iris-versicolor,[6.4,2.9,4.3,1.3])-->prob=[0.795868931454,0.204131068546],predictLabel=Iris-versicolor
(Iris-versicolor,[6.7,3.0,5.0,1.7])-->prob=[0.676938845836,0.323061154164],predictLabel=Iris-versicolor
(Iris-virginica,[4.9,2.5,4.5,1.7])-->prob=[0.676938845836,0.323061154164],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.4,3.8,1.1])-->prob=[0.841727580252,0.158272419748],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.5,4.0,1.3])-->prob=[0.795868931454,0.204131068546],predictLabel=Iris-versicolor
(Iris-versicolor,[5.5,2.6,4.4,1.2])-->prob=[0.819934748118,0.180065251882],predictLabel=Iris-versicolor
(Iris-versicolor,[5.7,2.6,3.5,1.0])-->prob=[0.861328953172,0.138671046828],predictLabel=Iris-versicolor
(Iris-versicolor,[5.8,2.7,3.9,1.2])-->prob=[0.819934748118,0.180065251882],predictLabel=Iris-versicolor
(Iris-virginica,[5.8,2.7,5.1,1.9])-->prob=[0.605700014665,0.394299985335],predictLabel=Iris-versicolor
(Iris-virginica,[5.8,2.8,5.1,2.4])-->prob=[0.414135982436,0.585864017564],predictLabel=Iris-virginica
(Iris-versicolor,[6.0,2.7,5.1,1.6])-->prob=[0.709915262079,0.290084737921],predictLabel=Iris-versicolor
(Iris-virginica,[6.1,3.0,4.9,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[6.3,2.8,5.1,1.5])-->prob=[0.740814410092,0.259185589908],predictLabel=Iris-versicolor
(Iris-virginica,[6.3,3.3,6.0,2.5])-->prob=[0.377041048688,0.622958951312],predictLabel=Iris-virginica
(Iris-virginica,[6.5,3.0,5.2,2.0])-->prob=[0.568084351171,0.431915648829],predictLabel=Iris-versicolor
(Iris-virginica,[6.5,3.0,5.5,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[6.7,2.5,5.8,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[6.9,3.1,5.4,2.1])-->prob=[0.529666704954,0.470333295046],predictLabel=Iris-versicolor
(Iris-virginica,[7.3,2.9,6.3,1.8])-->prob=[0.64210359201,0.35789640799],predictLabel=Iris-versicolor
(Iris-virginica,[7.4,2.8,6.1,1.9])-->prob=[0.605700014665,0.394299985335],predictLabel=Iris-versicolor


mlrAccuracy = evaluator.evaluate(mlrPredictions)

println("Test Error = " + str(1.0 - mlrAccuracy))
Test Error = 0.48730158730158735

mlrModel = mlrPipelineModel.stages[2]

print("Multinomial coefficients: " + str(mlrModel.coefficientMatrix)+"Multinomial intercepts: "+str(mlrModel.interceptVector)+"numClasses: "+str(mlrModel.numClasses)+"numFeatures: "+str(mlrModel.numFeatures))

Multinomial coefficients: 2 X 4 CSRMatrix
(0,3) -0.0776
(1,3) 0.0776Multinomial intercepts: [0.913185966051,-0.913185966051]numClasses: 2numFeatures: 4

​
​
子雨大数据之Spark入门
扫一扫访问本博客

© 2014 厦大数据库实验室